SDSU Logo

Main Content

example_2_2_mod

Contents

%
% An attempt at mixing symbolic and "numeric" computations using
% Matlab
%

%(sym) make x and y symbols
syms x y

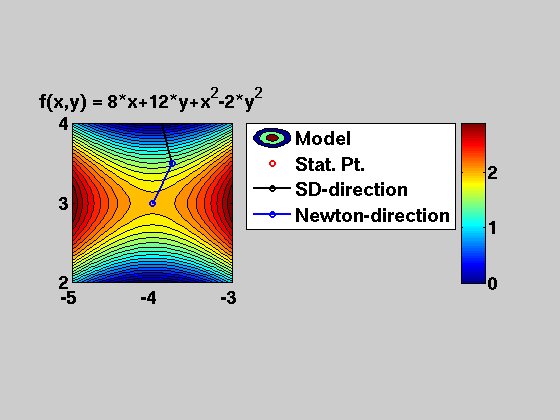
(part-a) The original silly objective of NW-2.2

%(sym) Function, Gradient, and Hessian
f1 = ( 8*x + 12*y + x.^2 - 2*y^2 )
f1_grad = [ diff(f1,x); diff(f1,y) ]
f1_hess = [ diff(diff(f1,x),x) diff(diff(f1,x),y); ...
	    diff(diff(f1,y),x) diff(diff(f1,y),y) ]

%(sym->num) Stationary Point
sp_1 = eval([ solve(f1_grad(1)); solve(f1_grad(2)) ])

%(num) Function, Gradient, and Hessian "inline functions."
f1_i      = inline(char(f1))
f1_grad_i = ...
    inline( [ '[' char(f1_grad(1)) ';' char(f1_grad(2)) ']' ] )
f1_hess_i = ...
    inline( [ '[[' char(f1_hess(1,1)) ' ' char(f1_hess(1,2)) '];' ...
	      '[' char(f1_hess(2,1)) ' ' char(f1_hess(2,2)) ']]' ], ...
	    'x','y')

%(num) Hessian evaluated at the stationary point
hess1_sp1 = f1_hess_i(sp_1(1),sp_1(2))

xv=(-1:0.05:1);
yv=(-1:0.05:1);
[X,Y] = ndgrid(xv,yv);
Z = zeros(size(X));
for i=1:size(X,1)
  for j=1:size(X,2)
    Z(i,j) = ...
	f1_i(sp_1(1),sp_1(2)) + ...
	1/2 * [xv(i) yv(j)] * f1_hess_i(sp_1(1),sp_1(2)) * [xv(i);yv(j)];
  end
end


%(plot)
figure(101)
contourf(X+sp_1(1),Y+sp_1(2),Z,25)
axis('square')
hold on;
plot(sp_1(1),+sp_1(2),'ro')
hold off
colorbar

% "Starting point for SD and Newton steps
xa1 = sp_1(1) + 0.25;
ya1 = sp_1(2) + 0.5;

ga1 = f1_grad_i(xa1,ya1)
ha1 = f1_hess_i(xa1,ya1)

sd1 = -ga1/norm(ga1);
nd1 = -ha1\ga1;
hold on
plot([xa1 xa1+sd1(1)],[ya1 ya1+sd1(2)],'ko-')
plot([xa1 xa1+nd1(1)],[ya1 ya1+nd1(2)],'bo-')
hold off

legend('Model','Stat. Pt.','SD-direction','Newton-direction',...
       'Location','NorthEastOutside')
title(['f(x,y) = ' char(f1)])

f1 =
8*x+12*y+x^2-2*y^2
f1_grad =
  8+2*x
 12-4*y
f1_hess =
[  2,  0]
[  0, -4]
sp_1 =
    -4
     3
f1_i =
     Inline function:
     f1_i(x,y) = 8*x+12*y+x^2-2*y^2
f1_grad_i =
     Inline function:
     f1_grad_i(x,y) = [8+2*x;12-4*y]
f1_hess_i =
     Inline function:
     f1_hess_i(x,y) = [[2 0];[0 -4]]
hess1_sp1 =
     2     0
     0    -4
ga1 =
    0.5000
   -2.0000
ha1 =
     2     0
     0    -4

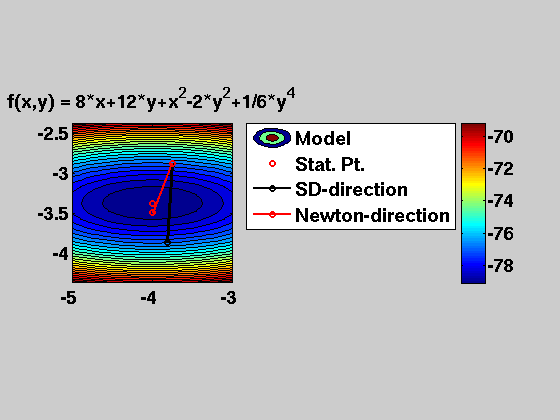
(part-b) Modified objective

%(sym) Function, Gradient, and Hessian
f2 = ( 8*x + 12*y + x.^2 - 2*y.^2 + (1/6)*y.^4 )
f2_grad = [ diff(f2,x); diff(f2,y) ]
f2_hess = [ diff(diff(f2,x),x) diff(diff(f2,x),y); ...
	    diff(diff(f2,y),x) diff(diff(f2,y),y) ]

%(sym->num) Stationary Point (select the only REAL one)
sp_2_x = eval([ solve(f2_grad(1)) ])
sp_2_y = eval([ solve(f2_grad(2)) ])
sp_2   = [ sp_2_x ; sp_2_y(1) ];

%(num) Function, Gradient, and Hessian "inline functions."
f2_i      = inline(char(f2))
f2_grad_i = ...
    inline( [ '[' char(f2_grad(1)) ';' char(f2_grad(2)) ']' ] )
f2_hess_i = ...
    inline( [ '[[' char(f2_hess(1,1)) ' ' char(f2_hess(1,2)) '];' ...
	      '[' char(f2_hess(2,1)) ' ' char(f2_hess(2,2)) ']]' ], ...
	    'x','y')

%(num) Hessian evaluated at the stationary point
hess2_sp2 = f2_hess_i(sp_2(1),sp_2(2))

xv=(-1:0.05:1);
yv=(-1:0.05:1);
[X,Y] = ndgrid(xv,yv);
Z = zeros(size(X));
for i=1:size(X,1)
  for j=1:size(X,2)
    Z(i,j) = ...
	f1_i(sp_2(1),sp_2(2)) + ...
	1/2 * [xv(i) yv(j)] * f2_hess_i(sp_2(1),sp_2(2)) * [xv(i);yv(j)];
  end
end

%(plot)
figure(201)
contourf(X+sp_2(1),Y+sp_2(2),Z,25)
axis('square')
hold on;
plot(sp_2(1),+sp_2(2),'ro')
hold off
colorbar

% "Starting point for SD and Newton steps
xa2 = sp_2(1) + 0.25;
ya2 = sp_2(2) + 0.5;

ga2 = f2_grad_i(xa2,ya2)
ha2 = f2_hess_i(xa2,ya2)

sd2 = -ga2/norm(ga2);
nd2 = -ha2\ga2;
hold on
plot([xa2 xa2+sd2(1)],[ya2 ya2+sd2(2)],'ko-')
plot([xa2 xa2+nd2(1)],[ya2 ya2+nd2(2)],'ro-')
hold off

legend('Model','Stat. Pt.','SD-direction','Newton-direction',...
       'Location','NorthEastOutside')
title(['f(x,y) = ' char(f2)])

f2 =
8*x+12*y+x^2-2*y^2+1/6*y^4
f2_grad =
          8+2*x
 12-4*y+2/3*y^3
f2_hess =
[        2,        0]
[        0, -4+2*y^2]
sp_2_x =
    -4
sp_2_y =
   -3.3681
  -63.2485
   66.6166
f2_i =
     Inline function:
     f2_i(x,y) = 8*x+12*y+x^2-2*y^2+1/6*y^4
f2_grad_i =
     Inline function:
     f2_grad_i(x,y) = [8+2*x;12-4*y+2/3*y^3]
f2_hess_i =
     Inline function:
     f2_hess_i(x,y) = [[2 0];[0 -4+2*y^2]]
hess2_sp2 =
    2.0000         0
         0   18.6885
ga2 =
    0.5000
    7.7435
ha2 =
    2.0000         0
         0   12.4522


Published with MATLAB® 7.6