lsq_examples.m --- Linear Least Squares examples.

Contents

Close all existing plots

close all

Defaults for plotting

set(0,'defaultlinelinewidth',2)
set(0,'defaultaxesfontsize',16)
set(0,'defaultaxesfontweight','bold')

Data points

x = [1.0 1.1 1.3 1.5 1.9 2.1]';
y = [1.84 1.90 2.31 2.65 2.74 3.18]';

Evaluation points

xv = 1.0:0.01:2.1;

Linear model

A1 = [ones(size(x)) x];
pcoef1 = A1\y;
p1 = polyval(flipud(pcoef1),xv);
y1 = polyval(flipud(pcoef1),x);
p1err = y1 - y;

% Plotting for linear model
figure
plot(xv,p1,'k-','linewidth',3); hold on;
for k=1:length(x)
  plot([x(k) x(k)],[y(k) y1(k)],'r-')
end
plot(x,y,'ko','linewidth',3); hold off
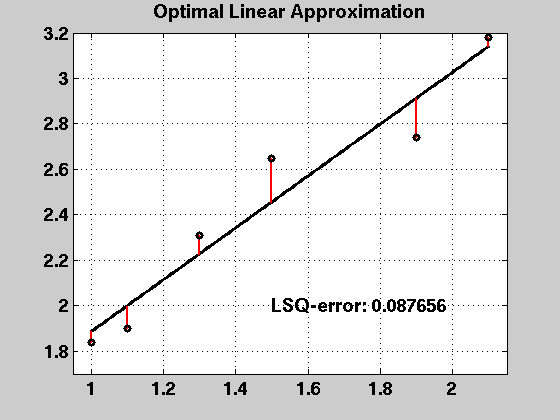
title('Optimal Linear Approximation')
axis([0.95 2.15 1.7 3.2]); grid on
text(1.5,2,sprintf('LSQ-error: %f',norm(p1err)^2), ...
     'FontWeight','Bold','FontSize',14)

fprintf('LSQ-error (squared): %f\n',sum(p1err.*p1err));
fprintf('cond(A1)           : %f\n',cond(A1));
fprintf('cond(A1''*A1)       : %f\n',cond(A1'*A1));

LSQ-error (squared): 0.087656
cond(A1)           : 8.246665
cond(A1'*A1)       : 68.007482

Quadratic model

A2     = [A1 x.*x];
pcoef2 = A2\y;
p2     = polyval(flipud(pcoef2),xv);
y2     = polyval(flipud(pcoef2),x);
p2err  = y2 - y;

% Plotting for quadratic model
figure
plot(xv,p2,'k-','linewidth',3); hold on;
for k=1:length(x)
  plot([x(k) x(k)],[y(k) y2(k)],'r-')
end
plot(x,y,'ko','linewidth',3); hold off
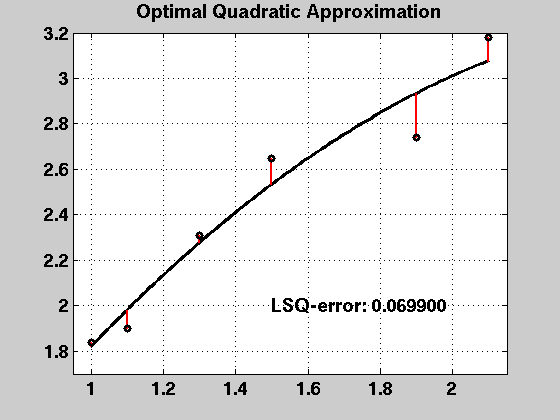
title('Optimal Quadratic Approximation')
axis([0.95 2.15 1.7 3.2]); grid on
text(1.5,2,sprintf('LSQ-error: %f',norm(p2err)^2), ...
     'FontWeight','Bold','FontSize',14)

fprintf('LSQ-error (squared): %f\n',sum(p2err.*p2err));
fprintf('cond(A2)           : %f\n',cond(A2));
fprintf('cond(A2''*A2)       : %f\n',cond(A2'*A2));

LSQ-error (squared): 0.069900
cond(A2)           : 111.908225
cond(A2'*A2)       : 12523.450801

Cubic model

A3     = [A2 x.*x.*x ];
pcoef3 = A3\y;
p3     = polyval(flipud(pcoef3),xv);
y3     = polyval(flipud(pcoef3),x);
p3err  = y3 - y;


% Plotting for cubic model
figure
plot(xv,p3,'k-','linewidth',3); hold on;
for k=1:length(x)
  plot([x(k) x(k)],[y(k) y3(k)],'r-')
end
plot(x,y,'ko','linewidth',3); hold off
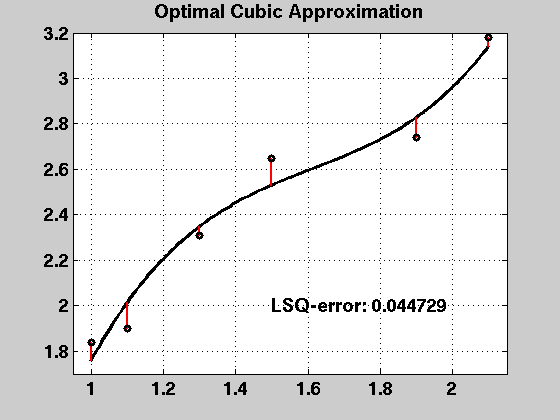
title('Optimal Cubic Approximation')
axis([0.95 2.15 1.7 3.2]); grid on
text(1.5,2,sprintf('LSQ-error: %f',norm(p3err)^2), ...
     'FontWeight','Bold','FontSize',14)

fprintf('LSQ-error (squared): %f\n',sum(p3err.*p3err));
fprintf('cond(A3)           : %f\n',cond(A3));
fprintf('cond(A3''*A3)       : %f\n',cond(A3'*A3));

LSQ-error (squared): 0.044729
cond(A3)           : 1670.659656
cond(A3'*A3)       : 2791103.686034

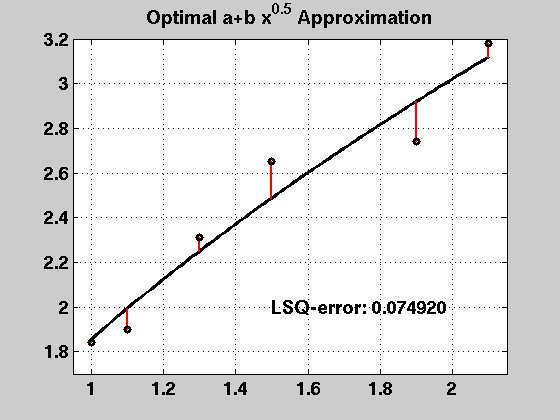
"Interesting" square-root model

A4     = [ones(size(x)) sqrt(x)];
pcoef4 = A4\y;
f4     = pcoef4(1) + pcoef4(2)*sqrt(xv);
y4     = pcoef4(1) + pcoef4(2)*sqrt(x);
p4err  = y4 - y;

% Plotting for square-root model
figure
plot(xv,f4,'k-','linewidth',3); hold on;
for k=1:length(x)
  plot([x(k) x(k)],[y(k) y4(k)],'r-')
end
plot(x,y,'ko','linewidth',3); hold off
title('Optimal a+b x^{0.5} Approximation')
axis([0.95 2.15 1.7 3.2]); grid on
text(1.5,2,sprintf('LSQ-error: %f',norm(p4err)^2), ...
     'FontWeight','Bold','FontSize',14)

fprintf('LSQ-error (squared): %f\n',sum(p4err.*p4err));
fprintf('cond(A4)           : %f\n',cond(A4));
fprintf('cond(A4''*A4)       : %f\n',cond(A4'*A4));

LSQ-error (squared): 0.074920
cond(A4)           : 15.109607
cond(A4'*A4)       : 228.300213

Exotic model

A5     = [ones(size(x)) x.^(3/2) 1./sqrt(x) exp(sin(x))];
pcoef5 = A5\y;
f5     = pcoef5(1) + pcoef5(2)*xv.^(3/2) + pcoef5(3)./sqrt(xv) + ...
	 pcoef5(4)*exp(sin(xv));
y5     = pcoef5(1) + pcoef5(2)*x.^(3/2) + pcoef5(3)./sqrt(x) + ...
	 pcoef5(4)*exp(sin(x));
p5err  = y5 - y;

% Plotting for exotic model
figure
plot(xv,f5,'k-','linewidth',3); hold on;
for k=1:length(x)
  plot([x(k) x(k)],[y(k) y5(k)],'r-')
end
plot(x,y,'ko','linewidth',3); hold off
axis([0.95 2.15 1.7 3.2]); grid on
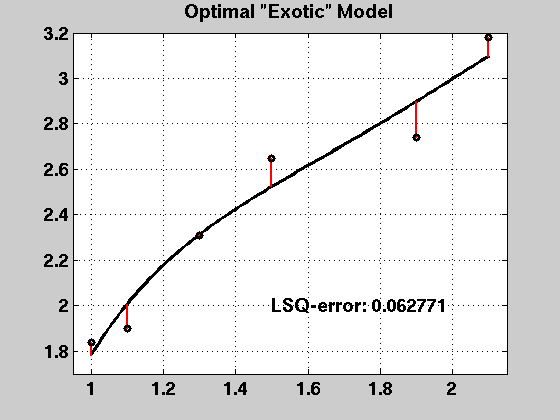
title('Optimal "Exotic" Model')
text(1.5,2,sprintf('LSQ-error: %f',norm(p5err)^2), ...
     'FontWeight','Bold','FontSize',14)

fprintf('LSQ-error (squared): %f\n',sum(p5err.*p5err));
fprintf('cond(A5)           : %f\n',cond(A5));
fprintf('cond(A5''*A5)       : %f\n',cond(A5'*A5));

LSQ-error (squared): 0.062771
cond(A5)           : 2208.908987
cond(A5'*A5)       : 4879278.912967

Published with MATLAB® 7.2