Contents
Chebyshev-Pade approximation of exp(-x) on [-1,1]
% % Display and plot options % format long format compact set(0,'defaultlinelinewidth',2) set(0,'defaultaxesfontsize',16) set(0,'defaultaxesfontweight','bold')
Input approximation order
fprintf('\nChebyshev-Pade Approx P_{n}(x)/Q_{m}(x) of exp(-x)\n'); fprintf(' m,n <= 4 works well, then we run into numerical trouble.\n'); n = 3; % input(' n = '); m = 3; % input(' m = '); n = n+1; % Add one for bookkeeping.
Chebyshev-Pade Approx P_{n}(x)/Q_{m}(x) of exp(-x)
m,n <= 4 works well, then we run into numerical trouble.
Inline functions
Tn(x) is the n:th Chebyshev Polynomial
fn(x) is exp(x)*Tn(x)/sqrt(1-x^2), the integrand which determines the coefficients for the Chebyshev expansion of exp(-x)
Tn = inline('cos(n*acos(x))','n','x'); f0 = inline('(1/pi)*exp(-x)./sqrt(1-x.^2)','x'); fn = inline('(2/pi)*exp(-x).*cos(n*acos(x))./sqrt(1-x.^2)','n','x');
Compute the coefficient in the Chebyshev expansion
fprintf('\nComputing Chebyshev-expansion coefficients...\n'); a = zeros(1+n+2*m,1); warning('off','all') a(1) = quad( f0, -1, 1, 1e-10 ); fprintf(' a_{0} = % 16.10e\n',a(1)); for k=1:(n+2*m) a(k+1) = quad( @(x)fn(k,x), -1, 1, 1e-10 ); fprintf(' a_{%d} = % 16.10e\n',k,a(k+1) ); end warning('on','all')
Computing Chebyshev-expansion coefficients...
a_{0} = 1.2660658610e+00
a_{1} = -1.1303181824e+00
a_{2} = 2.7149530568e-01
a_{3} = -4.4336824243e-02
a_{4} = 5.4742065953e-03
a_{5} = -5.4290073241e-04
a_{6} = 4.4943468284e-05
a_{7} = -3.1728559898e-06
a_{8} = 1.6535684447e-07
a_{9} = 1.4551009141e-08
a_{10} = -3.3304169159e-08
Build the matrix
N = length(a); A = zeros(n+m,n+m); for k=1:(n+m) a_order = (k-1); % Order to generate for q_order=1:m % q_order=j : q_j*T_j(x) a_index(1) = a_order + q_order; a_index(2) = a_order - q_order; a_index(3) = q_order - a_order; a_index = unique(a_index(find(a_index>=0))); for aix=1:length(a_index) if( (a_index(aix) >=0) & ((a_index(aix)+1) <= length(a)) ) if( a_index(aix)==0 ) dv = 1; else dv = 2; end A(k,q_order) = A(k,q_order) + a(a_index(aix)+1)/dv; end end end end A(1:n,m+(1:n)) = -eye(n);
Build the right-hand-side
b = - a(1:(n+m)); % % Solve % c=A\b; % % Extract the coefficients % P=[c((m+1):(m+n))]; Q=[1 ; c(1:m)]; % % Compute the numerator and denominator % xv = -1:0.01:1; num = 0; for k=1:length(P) num = num + P(k) * Tn(k-1,xv); end den = 0; for k=1:length(Q) den = den + Q(k) * Tn(k-1,xv); end r = num./den;
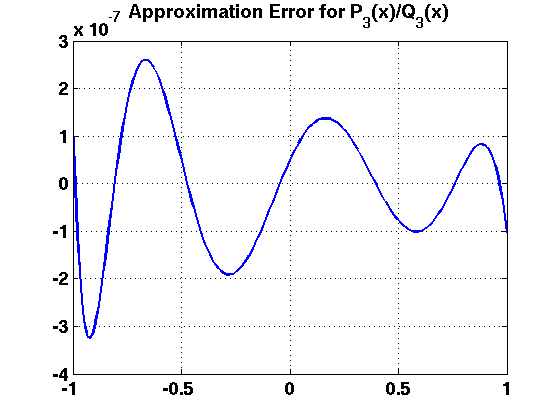
Plot the approximation error
plot(xv,r-exp(-xv),'b-') grid on title(sprintf('Approximation Error for P_{%d}(x)/Q_{%d}(x)',n-1,m))